Introduction

La cryptographie à algorithmes symétriques utilise la même clé pour les processus de codage et de décodage ; cette clé est le plus souvent appelée « secrète » (en opposition à « privée ») car toute la sécurité de l’ensemble est directement liée au fait que cette clé n’est connue que par l’expéditeur et le destinataire. Ce type de cryptographie fonctionne habituellement suivant deux procédés différents, le cryptage par blocs (DES, AES, Skipjack…); et le cryptage en continu « stream » (algorithme RC4) et font souvent appel à des algorithmes de génération de nombres aléatoires nécessitant de l’aléa.

Une bonne distribution statistique ne suffit pas en cryptographie. L’aléa cryptographique doit également être imprédictible.

Les utilisations de nombres aléatoires en cryptographie sont diverses : génération de clés, génération de vecteurs d’initialisation en cryptographie symétrique, randomisation en cryptographie asymétrique. Des tests statistiques permettent de vérifier la bonne distribution statistique de l’aléa généré, mais aucun des tests existants ne garantit l’imprévisibilité d’une source de nombres aléatoires. Le caractère imprédictible de l’aléa cryptographique ne s’étudie pas sur la suite de bits générée mais sur l’algorithme de génération. D’une manière générale, il est recommandé de retraiter l’aléa issu d’une source aléatoire non maîtrisée pour en garantir l’imprédictibilité.

Les mécanismes cryptographiques présentés précédemment agissent sur des données de format bien défini. La définition des algorithmes de chiffrement par bloc induit une manière naturelle de chiffrer des blocs de taille fixe. Il existe cependant différentes manières d’utiliser ces primitives pour chiffrer des messages de taille quelconque, appelées modes opératoires. Historiquement, les modes d’opération ont été abondamment étudiés pour leurs propriétés de propagation d’erreurs lors de divers scénarios de modification de données durant le chiffrement. Le mode le plus naturel consiste à découper le message en blocs de n bits, et à appliquer la fonction de chiffrement à chacun de ces blocs avec la clé de chiffrement

• Ce mode est appelé ECB (Electronic CodeBook). Il ne doit pas être utilisé, car les messages chiffrés obtenus laissent fuir de l’information sur les messages clairs correspondants.

En effet, deux blocs de clair identiques conduisent à deux blocs de chiffré identiques. Il y’a autres modes par bloc qui sont utilisés comme : Cipher Block Chaining (CBC), Cipher FeedBack (CFB) ou Output FeedBack (OFB).

Dans cet article, on va essayer de présenter le principe de fonctionnement de Cipher Block Chaining (CBC), et on va présenter une application qui illustre les modes de cryptement de César et Vigenère.

Introduction à la cryptographie

Modes de chiffrement par blocs (CBC)

CBC(Cipher Block Chaining)

I.                    Modes de chiffrement par blocs :

Avant de s’intéresser à la construction de l’algorithme de chiffrement par blocs lui-même, il est utile de préciser qu’il existe plusieurs modes qui permettent d’enchaîner le chiffrement des différents blocs de taille n, mi pour i variant de 0 à t−1, la fonction de chiffrement EK s’appliquant alors à chacun des blocs. Il s’agit donc de chaîner les ci =EK (mi) avec en général mi+1 pour i variant de 0 à t−1. Où K désigne la clé utilisée par l’algorithme, E désigne le cryptage en lui-même, M (ou m, mi) désigne le message en clair (c’est-à-dire un bloc) et C (ou c, ci) le chiffré résultant. Toutefois, tous les algorithmes ne permettent pas d’utiliser tous les modes possibles. On peut citer : le mode CBC de l’anglais Cipher Block chaining qui utilise un chiffrement à enchaînement. Pour mieux comprendre, voyons ce mode plus en détails.

1. I.1   Cipher Block chaining (CBC):

1. I.1.1   Description du mode opératoire

Le mode de chiffrement très employé est le mode CBC (enchaînement des blocs). Il consiste à chiffrer le bloc i préalablement combiné par ou exclusif avec le chiffré du bloc précédent ainsi,

ci = EK(mi ⊕ci−1) pour tout i de 1 à t, avec c0 = EK(m0 ⊕IV) où IV désigne un vecteur d’initialisation. C’est un bloc de données aléatoires qui permet de commencer le chiffrement du premier bloc et qui fournit ainsi une forme de hasard indépendant du document à chiffrer. Il n’a pas besoin d’être lui-même chiffré lors de la transmission, mais il ne doit jamais être réemployé avec la même clé. Dans ce mode, on applique sur chaque block un ‘OU exclusif’ avec le chiffrement du bloc précédent avant qu’il soit lui-même chiffré. De plus, afin de rendre chaque message unique, un vecteur d’initialisation (IV) est utilisé. Ce vecteur d’initialisation change à chaque session, et doit être transmis au destinataire. Par contre, il n’est pas nécessaire de le chiffrer avant de l’envoyer : il peut être connu de l’adversaire.

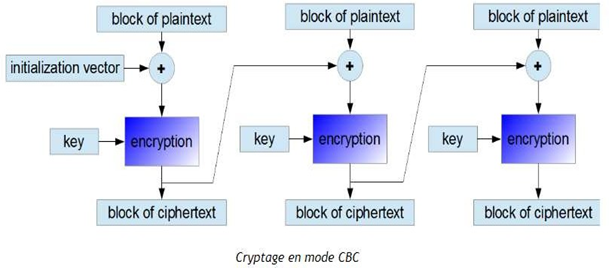
Pour déchiffrer un bloc de texte chiffré en mode CBC, on applique l’algorithme de déchiffrement au bloc chiffré et puis on le combine par ou exclusif avec le bloc chiffré précédent, respectivement avec le vecteur d’initialisation, dans le cas du premier bloc. On effectue donc les opérations suivantes :

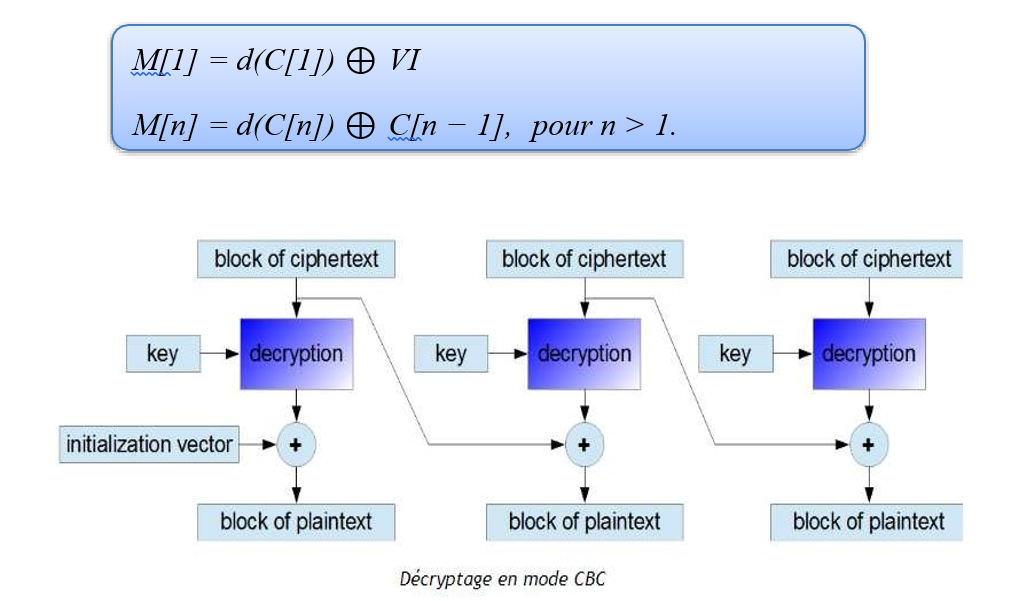
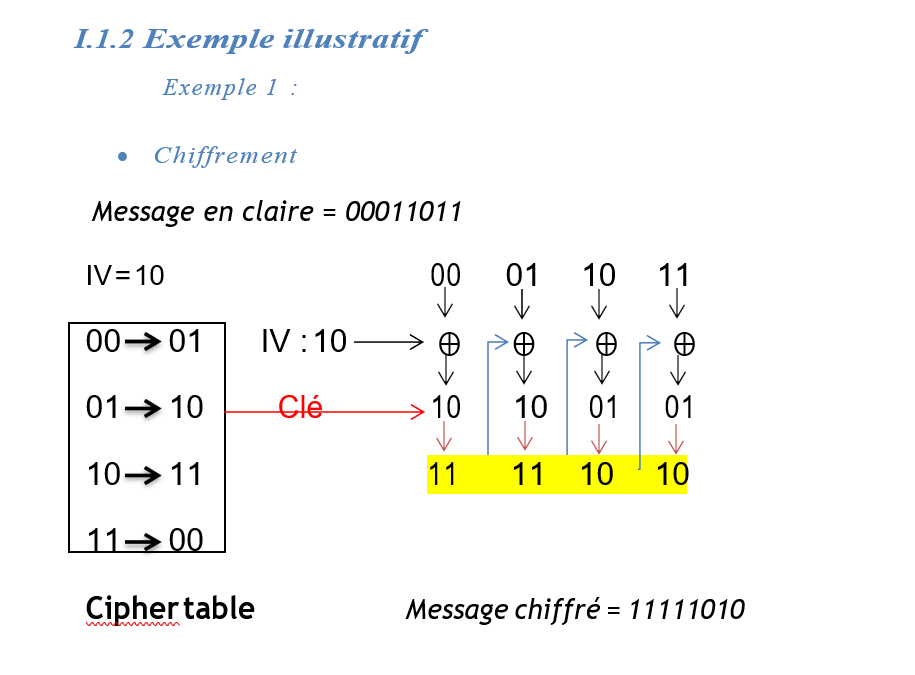
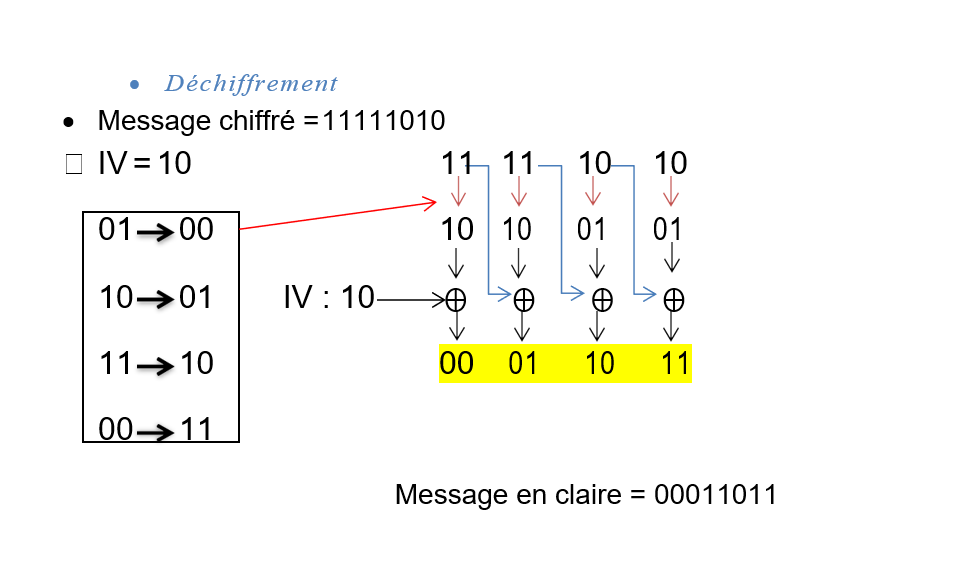
I.1.1   Les avantages et les inconvénients

I.1.3.1 Avantages

Ce mode a plusieurs avantages, et aussi un gros inconvénient. Le mode CBC chiffre le même message clair différemment avec des blocs d’initialisation différents. De plus, le chiffrement d’un bloc dépend également des blocs précédents, et par conséquent, si l’ordre des blocs du cryptogramme est modifié, le déchiffrement est impossible et le destinataire se rend compte du problème. De plus, si une erreur de transmission affecte le bloc chiffré ci, alors seuls les blocs mi et mi+1 seront affectés, les autres blocs seront déterminés correctement.

1.1.3.2 Inconvénients

L’inconvénient principal de ce mode est sa lenteur. Imaginons que l’on veuille faire du chiffrement/déchiffrement en temps réel, et en simultané (cas par exemple d’une communication téléphonique) et que les algorithmes de chiffrement et de déchiffrement CK et DL soient assez longs à mettre en œuvre. Alors le destinataire, pour commencer le déchiffrement de ci, doit attendre d’avoir terminé celui de ci−1. Ainsi, le temps écoulé entre le chiffrement et le déchiffrement avec le mode CBC peut être trop long pour ce genre d’applications.

I.1.2     Considérations de sécurité

Le rôle du vecteur d’initialisation est d’empêcher que si deux textes en clair débutent de la même façon, les textes chiffrés correspondants le font également. Il n’est pas obligatoire de le choisir aléatoirement ; il peut aussi être un numéro d’ordre qui est augmenté après chaque message. La seule chose importante est qu’il doit être différent pour chaque message chiffré avec la même clé. Grâce au vecteur d’initialisation, même un bloc de texte en clair identique donnera un message chiffré différent. Il n’est plus possible pour un espion d’apprendre la moindre information concernant le texte en clair à partir du texte chiffré. Il n’est pas nécessaire non plus de tenir secret le vecteur initialisation. Généralement on le transmet en clair avec le texte chiffré.

I.1.3    Propagation d’erreurs

Une erreur d’un simple bit dans le texte chiffré, par exemple dû à un bruitage de la liaison ou d’un disfonctionnement du dispositif de stockage, affecte un bloc et un bit du texte en clair reconstruit. En effet, le bloc contenant l’erreur est complètement brouillé et de plus il apparaît une erreur d’un bit dans le bloc suivant au même endroit que le bit erroné. Les autres blocs ne sont pas affectés par l’erreur ; on dit que le mode CBC est auto-récupérant.

CBC(Cipher Block Chaining)

Le mode de chiffrement avec chaînage de blocs ne récupère par contre pas du tout les erreurs de synchronisation. Si un bit est ajouté ou perdu dans le flot de texte chiffré, alors tous les blocs qui suivent sont décalés d’un bit et deviennent indéchiffrables. A cause de ce phénomène d’amplification d’erreur, tout cryptosystème qui utilise le mode CBC doit s’assurer que la structure des blocs reste intacte, soit par encadrement soit en stockant les données dans des paquets de plusieurs blocs. Généralement, on ajoute un système de détection d’erreurs et des méthodes de récupération à la ligne de communication qu’on applique après le chiffrement et avant le déchiffrement.

Fin 2001, Serge Vaudenay a trouvé une attaque contre l’implémentation de certains systèmes qui utilisent le mode CBC pour chiffrer des messages préformatés et qui testent après le déchiffrement si le texte en clair récupéré est bien du bon type. En exploitant le protocole de communication de tels systèmes, on peut, sous certaines conditions assez restrictives, déchiffrer les messages chiffrés, sans connaître la clé de chiffrement. Martin Vuagnoux a publié en février 2003 un programme qui permettait d’attaquer l’OpenSSL en mode CBC.

On peut cependant éviter cette attaque, ou bien en appliquant une fonction de hachage au texte rembourré avant de le chiffrer ou bien en remplaçant le mode CBC par un mode qui garantit l’authenticité et la confidentialité des messages, comme le mode OCB (les nouvelles versions 0.9.6i et 0.9.7 de OpenSSL ne sont d’ailleurs plus vulnérables par cette attaque).

I.1.4 Cryptanalyse

Attaque distinctive (distinguishing attack) : En cryptographie, une attaque distinctive est toute forme d’analyse cryptographique sur des données chiffrées par un chiffrement qui permet à un attaquant de distinguer les données chiffrées des données aléatoires. Les chiffrements symétriques à clé moderne sont spécifiquement conçus pour être immunisés contre une telle attaque. En d’autres termes, les schémas de chiffrement modernes   sont   des permutations   pseudo – aléatoires et   sont   conçus   pour    avoir une indiscernabilité indiscernable . Si on trouve un algorithme capable de distinguer la sortie d’aléatoire de manière plus rapide qu’une recherche par force brute , cela est considéré comme une rupture du chiffre.

Attaque par cryptogramme (ciphertext-only attack (COA) or known ciphertext attack) : est un modèle d’attaque pour la cryptanalyse dans laquelle l’attaquant est supposé avoir accès uniquement à un ensemble de textes cryptés.. Bien que l’attaquant ne dispose d’aucun canal fournissant l’accès au texte en clair avant le cryptage, dans toutes les attaques pratiques utilisant uniquement un cryptogramme, l’attaquant a toujours une certaine connaissance du texte en clair. Par exemple, l’attaquant pourrait connaître la langue dans laquelle le texte en clair est écrit ou la distribution statistique attendue des caractères du texte en clair. Les données et les messages de protocole standard font généralement partie du texte en clair dans de nombreux systèmes déployés et peuvent généralement être devinés ou connus de manière efficace dans le cadre d’une attaque utilisant uniquement un texte chiffré sur ces systèmes.

Attaque en texte connu (known-plaintext attack (KPA)) : est un modèle d’attaquepour l’ analyse cryptée où l’attaquant a accès à la fois au texte en clairet à sa version chiffrée ( texte chiffré ). Ceux-ci peuvent être utilisés pour révéler d’autres informations secrètes telles que des clés secrètes et des livres de codes .

Attaque par type de texte en clair (chosen-plaintext attack (CPA)) : est un modèle d’ analyse cryptographique qui suppose que l’attaquant peut choisir de chiffrer des textes en clair au hasard et obtenir les textes chiffrés correspondants . L’attaque a pour objectif d’obtenir des informations supplémentaires qui réduisent la sécurité du schéma de chiffrement. Dans le pire des cas, une attaque par texte en clair choisi pourrait révéler des informations secrètes après le calcul de la clé secrète .