Introduction à la Cryptographie

• Cryptographie : La cryptographie est l’ensemble des techniques qui permettent de rendre un message inintelligible.
• Cryptanalyse : la science qui consiste à tenter de déchiffrer un message ayant été chiffré sans posséder la clé de chiffrement
• Cryptologie : la science des messages secrets. Elle se décompose en deux disciplines: la cryptographie et la cryptanalyse.
• Chiffrement : Ensemble de procédés et ensemble de symboles (lettres, nombres, signes, etc.) employés pour remplacer les lettres du message à chiffrer.
• Codage : Ensemble de procédés et ensemble de symboles (lettres, nombres, signes, etc.) employés pour remplacer les mots du message à coder.
• Déchiffrement :le procédé consistant à retrouver le texte original en possédant la clé de (dé)chiffrement
• Décryptage: consiste à retrouver le texte original à partir d’un
message chiffré sans posséder la clé de (dé)chiffrement
• Sténographie : branche particulière de la cryptographie qui consiste à camoufler le message dans un support (texte, image, etc.) de manière à masquer sa présence.
La cryptographie
• Le cryptage – décryptage s’effectue au moyen d’une clef de chiffrement
ou de déchiffrement.
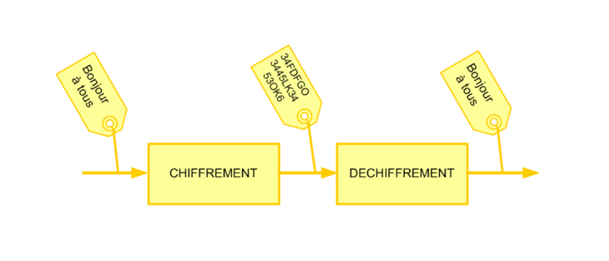
Service de la cryptographie
• La cryptographie permet d’assurer
– la confidentialité des données: personne n’a le droit de lire les données.
– L’intégrité: personne ne pourra modifier les données.
– L’authenticité: personne ne pourra contrefaire l’origine des données.

Un peu d’histoire
Grèce antique : La scytale utilisée à Sparte :
– Algorithme : Texte écrit sur un ruban enroulé autour d’un bâton
– Clé : diamètre du bâton Le chiffrement de la substitution par décalage / Chiffre -code de César
– Chaque lettre correspond à la lettre n fois plus loin dans l’alphabet
• Pour N=5 , A=F , B=G, etc
– Facilement déchiffrable lorsque la langue est connue
– Exemple : montrer qu’il est très aisé de déchiffrer le message
suivant (écrit en français) : Sloasb gsqifwhs fsgsoi.
Cryptage par clé
Il existe deux catégories de chiffrement
• Symétrique (Utilisation d’une clé secrète)
• Asymétrique (Utilisation de clés publiques)

Cryptographie symétrique
• La cryptographie symétrique ou « à secret partagé » utilise
la même clé pour le chiffrement et le déchiffrement

Caractéristiques du chiffrement symétrique
• Avantages:
– Système rapide pour l’implémentation matérielle
– Clés relativement courtes (64, 128, etc.)
• Inconvénients:
– Gestion des clés difficiles (plusieurs clés)
– Transmission de clé ( échange d’un secret =point faible)
Cryptographie symétrique : DES Data Encryption Standard (DES ):
– Chiffrement par bloc de 64 bits
– Publié en 1977 par IBM Corp
– Désormais remplacé par Advanced Encryption Standard (AES)
Utilise une clé de longueur fixe
• 56 bits générés aléatoirement dans une clé de 64 bits
• 8 bits servant à la parité (8, 16, 24, 32, 40, 48, 56)
DES n’est pas fiable et peu performant : cassé en 22h en 1999
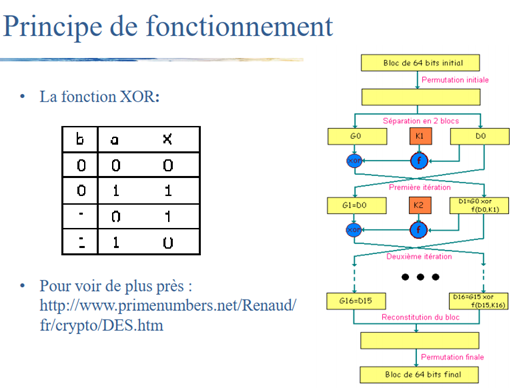
Principe de fonctionnement
• Phase 1 : Préparation – Diversification de la clé. Découper le texte en bloc de 64 bits et fabriquer à partir de K 16 sous-clés K1,…,K16 de 48 bits.
• Phase 2 : Permutation initiale.
Pour chaque bloc de 64 bits du texte, on calcule une permutation Y=P(X). Y est représenté sous la forme Y=G0D0, G0 étant les 32 bits à gauche de y, D0 les 32 bits à droite.
• Phase 3 : Itération – schéma de Feistel
On applique 16 tours d’un même schéma de Feistel. A partir de Gi-1Di-1 (pour i de 1 à 16), on calcule GiDi en posant :
– Gi=Di-1;
– Di=Gi-1⊕f(Di-1,Ki)
• Phase 4 : Permutation finale.
On applique à G16D16 l’inverse de la permutation initiale. Z=P-1(G16D16) est le bloc de 64 bits chiffré à partir de x.
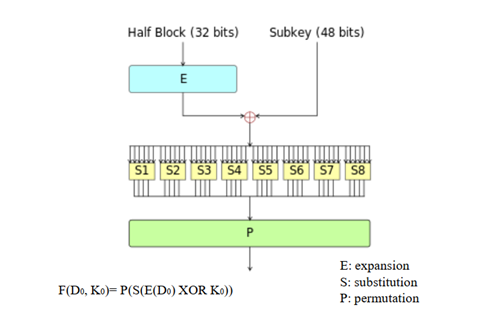
La fonction Feistel
Cryptographie symétrique : AES
Advanced Encryption Standard remplace DES
Standard du gouvernement américain
Utilise l’algorithme de Rijndael
Chiffrement par blocs
La longueur de la clé et des blocs sont des multiples de 32 bits
La clé peut être128 bits, 192 bits ou bien 256 bits
Les blocs de données sont fixé à 128 bits
Nombre de cycle entre 10, 12 et 14
Pour les curieux http://people.eku.edu/styere/Encrypt/JSAES.html
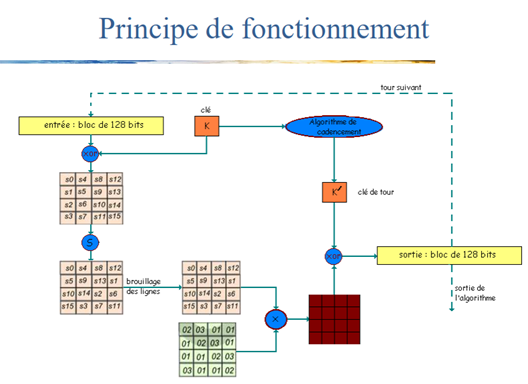
Principe de fonctionnement
• Découpage du texte en blocs de 128 bits, avec une clé de 128 bits
également. Chaque bloc subit une séquence de 5 transformations
répétées 10 fois
1. Addition de la clé secrète (par un ou exclusif).
2. Transformation non linéaire d’octets : les 128 bits sont répartis en 16
blocs de 8 bits (8 bits=un octet), eux-même dispatchés dans un tableau
4×4. Chaque octet est transformé par une fonction non linéaire S.
3. Décalage de lignes : les 3 dernières lignes sont décalées cycliquement
vers la gauche : la 2ème ligne est décalée d’une colonne, la 3ème ligne
de 2 colonnes, et la 4ème ligne de 3 colonnes.
4. Brouillage des colonnes : Chaque colonne est transformée par
combinaisons linéaires des différents éléments de la colonne (ce qui
revient à multiplier la matrice 4×4 par une autre matrice 4×4).
5. Addition de la clé de tour : A chaque tour, une clé de tour est générée à
partir de la clé secrète par un sous-algorithme (dit de cadencement).
Cette clé de tour est ajoutée par un ou exclusif au dernier bloc obtenu.
Cryptage asymétrique
• La cryptographie asymétrique, ou cryptographie à clé publique
repose sur l’utilisation d’une clé publique et d’une clé privée l’une
permettant de coder le message et l’autre de le décoder.
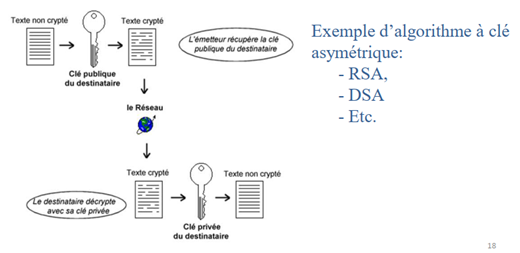
Cryptage asymétrique
• Résout le problème de la distribution de la clé
• Les deux clés forment une paire

• Seul le détenteur de la clé privée peut déchiffrer le message
• Impossible de trouver la clé privée en partant de la clé publique
• Sécuriser l’échange de la clé publique n’est pas nécessaire
• La clé privée n’est pas transmise
RSA
• RSA : algorithme a été décrit en 1977 par Ronald Rivest, Adi
Shamir et Leonard Adleman
• Le système le plus répandu et le plus utilisé
• Utilise des longueurs de clé arbitraire
• Longueur standard de 512 bits
• RSA est lent comparé à la cryptographie symétrique
• Utilisé pour chiffrer une clé secrète plutôt que le message
• La clé chiffrée est alors la clé de session
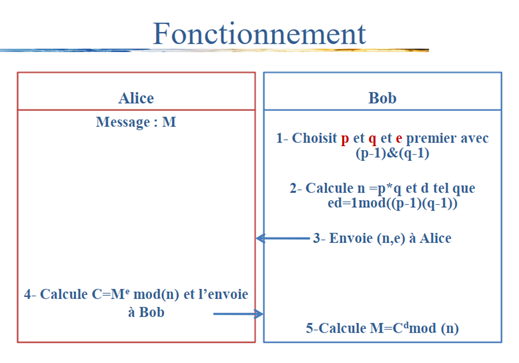
Principe
• Soit M le message à chiffrer et C le message chiffré.
• Pour chiffrer le message, on calcule :
– C = Me modulo n.
• Pour déchiffrer on calcule :
– M = Cd modulo n.
• La clé publique est :
– le couple (e,n)
• La clé privée est :
– le couple (d,n).
• Comment procède-t-on pour former les couples (e,n) et
(d,n).
– On choisit au hasard 2 grands nombres premiers p et q.
– On calcule n = p.q
– On pose j = (p-1).(q-1)
– On sélectionne e tel que : e et j soient premiers entre
eux avec 1 < e < j .
– On calcule d tel que : e.d = 1 mod j (e et d sont
inverses l’un de l’autre modulo j)
Exemple
• Prenons p = 47 , q = 59 et e =17
Utilisé l’algorithme RSA pour chiffrer et déchiffrer le message
M = 01000010
– On calcule n = p.q = 47.59 = 2773
– On calcule alors, d tel que d.e = 1 mod (p – 1)(q – 1), soit d = 157.
Clef publique : (e, n) = (17, 2773)
Clef privé : d = 157.
– Chiffrement du message M = 01000010 = 66 :
C = (Me mod n) = (6617 mod 2773) = 872
– Déchiffrement de C :
(C d mod n) = (872157 mod 2773) = 66
Inconvénient RSA
• Complexité algorithmique de la méthode:
– recherche de nombres premiers de grande taille, et choix de clés très
longue
• Réalisation des opérations modulo n.
– Problème d’implémentation sur les équipements disposants de faible
puissance de calcul (ex: cartes bancaire, stations mobiles, etc.)
– La méthode est officiellement sûre si des contraintes de longueur des clés
et d’usage sont respectées.
• Solution: Utilisation de RSA pour l’échange des clés
secrètes de session d’un algorithme symétrique à clés privées
Le hachage
• Fonction de hashage ou fonction de condensation, permet à partir d’un texte de
longueur quelconque, de calculer une chaîne de taille inférieure et fixe appelé
condensé ou empreinte (message digest ou hash en anglais)
• Une fonction de hachage est :
– à sens unique, c’est à dire qu’à partir du message haché, il est impossible de
retrouver le message original.
– sans collisions, impossibilité de trouver deux messages distincts ayant la
même valeur de condensé. La moindre modification du message entraîne la
modification de l’empreinte.
– Le message haché est de taille fixe (16 ou 20 octets)
• Exemples :
– MD5 (Message Digest 5 – Rivest1991-RFC 1321) : calcul une empreinte de
128 bits
– SHA-1 (Secure Hash Algorithm 1 – NIST1994) : plus sûr que MD5 –
empreinte de 160 bits
26
• Utilisée seule, elle permet de vérifier l’intégrité d’un message.
• Associé à un chiffrement asymétrique, elle permet le calcul de signatures, pour
assurer :
– Intégrité des données
– Authentification de la source
– Non-répudiation de la source
