Les machines vectorielles de support sont des algorithmes d’apprentissage automatique très polyvalents. La principale raison de leur popularité est leur capacité à effectuer à la fois une classification et une régression linéaires et non linéaires en utilisant ce que l’on appelle l’astuce du noyau; si vous ne savez pas ce que c’est, ne vous inquiétez pas. À la fin de cet article, vous serez en mesure de:
- Comprendre ce qu’est un SVM et son fonctionnement
- Distinguer entre un SVM à marge ferme et un SVM à marge souple
- Coder un SVM à partir de zéro en Python
- Alors, sans plus tarder, plongeons-nous!
Qu’est-ce qu’un SVM et pourquoi en ai-je besoin?
Avec tant d’autres algorithmes (régression linéaire, régression logistique, réseaux de neurones, etc.), vous vous demandez peut-être pourquoi vous devez en avoir un autre dans votre boîte à outils! Peut-être que ces questions peuvent être répondues à l’aide d’un diagramme:
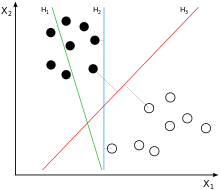
Ici, nous voyons trois limites de décision potentielles pour classer les données: H1, H2 et H3. Tout d’abord, H1 ne sépare pas du tout les classes, donc ce n’est pas un bon hyperplan. H2 sépare les classes, mais remarquez à quel point la marge (ou la rue) entre les points est si petite, et ce classificateur est très peu susceptible de bien fonctionner sur des instances invisibles.
Le troisième hyperplan, H3, représente la frontière de décision du classifieur SVM; Cette ligne sépare non seulement les deux classes mais garde également la distance la plus large entre les points les plus extrêmes des deux classes.
Vous pouvez considérer le SVM comme une marge la plus large possible entre les deux classes. C’est ce qu’on appelle la classification des grandes marges.
Classification des grandes marges

Comme je l’ai dit, un classificateur SVM à grande marge essaie essentiellement de s’adapter à la rue la plus large possible (indiquée par les lignes parallèles en pointillés) entre deux classes. Il est important de noter que l’ajout d’instances « hors rue » (pas sur la ligne en pointillés) n’affectera pas la limite de décision.
La frontière de décision est entièrement déterminée (ou supportée) par les instances les plus extrêmes de la classe, ou, en d’autres termes, les instances situées en bordure de rue. Ceux-ci sont appelés vecteurs de support (ils sont entourés en noir dans le diagramme).
Limites de la classification de la marge dure
Donc, essentiellement, un SVM à marge rigide essaie fondamentalement d’ajuster une frontière de décision qui maximise la distance entre les vecteurs de support des deux classes. Cependant, il y a quelques problèmes avec ce modèle:
- Il est très sensible aux valeurs aberrantes
- Cela ne fonctionne que sur les données séparables linéairement
Ces deux concepts peuvent être clairement mis en évidence dans cette visualisation:
Problème 1: il est très sensible aux valeurs aberrantes
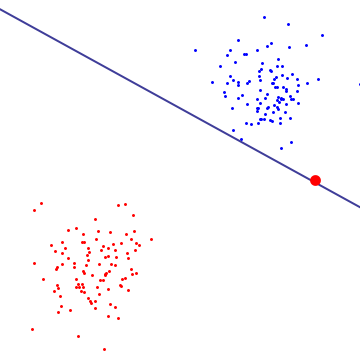
Notez que le point rouge est une valeur aberrante extrême, et par conséquent, l’algorithme SVM l’utilise comme vecteur de support. Étant donné que le classificateur Hard Margin trouve la distance maximale entre les vecteurs de support, il utilise les vecteurs de support rouge et bleu pour définir une limite de décision.
Il en résulte une très mauvaise limite de décision qui est probablement surajustée et ne permettra pas de bien prédire les nouvelles classes.
Problème 2: cela ne fonctionne que sur des données séparables linéairement

Dans cet exemple, nous pouvons clairement observer qu’il n’y a pas de classificateur linéaire possible qui séparera les classes. De plus, il existe une valeur aberrante majeure. La question est donc de savoir comment un SVM peut séparer des données séparables de manière non linéaire?
Traitement des valeurs aberrantes et des données non linéaires

Une approche consiste à trouver un bon équilibre entre garder les rues aussi larges que possible (maximiser la marge) et limiter les violations de marge (ce sont des cas qui se retrouvent au milieu de la rue ou même du mauvais côté de la rue). C’est ce qu’on appelle un SVM à marge souple.
Vous contrôlez essentiellement le compromis entre deux objectifs:
- Maximiser la distance entre la frontière de décision et les vecteurs de support
- Maximiser le nombre de points correctement classés par la frontière de décision
Ce compromis est généralement contrôlé par un hyperparamètre qui peut être désigné par λ, ou, plus communément (dans scikit-learn) le paramètre C. Cela contrôle essentiellement le coût des erreurs de classification. Concrètement,
- Une petite valeur de C conduit à une rue plus large mais plus de violations de marge (biais plus élevé, variance plus faible)
- Une valeur élevée de C conduit à une rue plus étroite mais avec moins de violations de marge (biais faible, variance élevée).
Bien que cette approche puisse fonctionner, nous devons déterminer le paramètre C optimal en utilisant des techniques de validation croisée. Cela peut prendre un temps considérable. De plus, on peut souhaiter créer un modèle optimal et ne pas avoir de variables «de marge» qui traversent les violations de marge. Alors, quelle est notre solution maintenant?
Approche deux: les noyaux

Bien que les SVM linéaires fonctionnent bien dans la plupart des cas, il est extrêmement rare d’avoir un jeu de données séparable linéairement. Une approche pour lutter contre cela consiste à ajouter plus de fonctionnalités, telles que des entités polynomiales (les thèses transforment essentiellement vos entités en élevant les valeurs à un polynôme à N degrés (pensez X², X³, etc.)).
Par exemple, disons que nous avons les données suivantes:
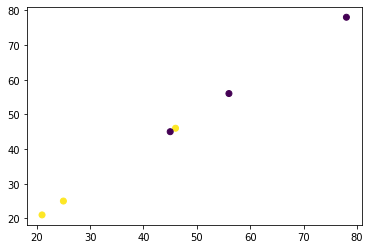
De toute évidence, cet ensemble de données n’est pas séparable de manière linéaire.
Cependant, lorsque nous appliquons une transformation polynomiale en élevant la racine à une puissance de 20:

Nous obtenons un ensemble de données séparable linéairement.
Cependant, cela n’est pas possible pour les grands ensembles de données; la complexité de calcul et le temps qu’il faudra pour que la transformation polynomiale se produise seraient tout simplement trop longs et coûteux en calcul.
De plus, l’utilisation de degrés polynomiaux d’ordre élevé crée un grand nombre de caractéristiques, ce qui rend le modèle trop lent.
C’est là que la beauté des SVM entre en jeu. Plus précisément, la beauté de l’astuce du noyau
L’astuce du noyau
à suivre …
